זו עדיין תיאוריה של LCAO-MO, אבל פשוט טיפשה למטה. ההבדל הוא שבמקום להזין את האורביטלים האטומיים "הטהורים" במנגנון ה- LCAO, אתה מבצע צעד מתמטי נוסף על מנת לקבל מסלולים בעלי תכונות כיווניות נחמדות, ואתה מזין את אלה במקום זאת, מנגנון LCAO.
בואו נדבר על דוגמה פשוטה, מתאן. אתה יכול להכיל את המסלולים $ \ mathrm {2s} $ ו- $ \ mathrm {2p} $ על פחמן כדי להשיג קבוצה של ארבעה היברידיות $ \ mathrm {sp ^ 3} $. אם כעת תנסה להפיק את הסימטריה של הכלאות $ \ mathrm {sp ^ 3} $ אלה, תבין שהם הופכים להיות $ A_1 + T_2 $. ואם אתה לא טרחת לעשות את שלב ההכלאה, נחשו מהן הסימטריות של מסלולי $ \ mathrm {2s} $ ו- $ \ mathrm {2p} $? מסלול $ \ mathrm {2s} $ הופך כ- $ A_1 $ והמסלול $ \ mathrm {2p} $ הופך ל- $ T_2 $. בסופו של דבר, אתה מקבל בערך את התמונה אותה דרך MOT, בין אם אתה משתמש במסלולים הכלאיים או לא. (שים לב שה $ 4 \ mathrm {sp ^ 3} $ בתרשים השני לא מציין מספר קוונטי ראשי של $ 4 $, אלא שיש ארבעה מסלולים כאלה. הייתי צריך לשנות את זה, אבל הייתי עצלן.)
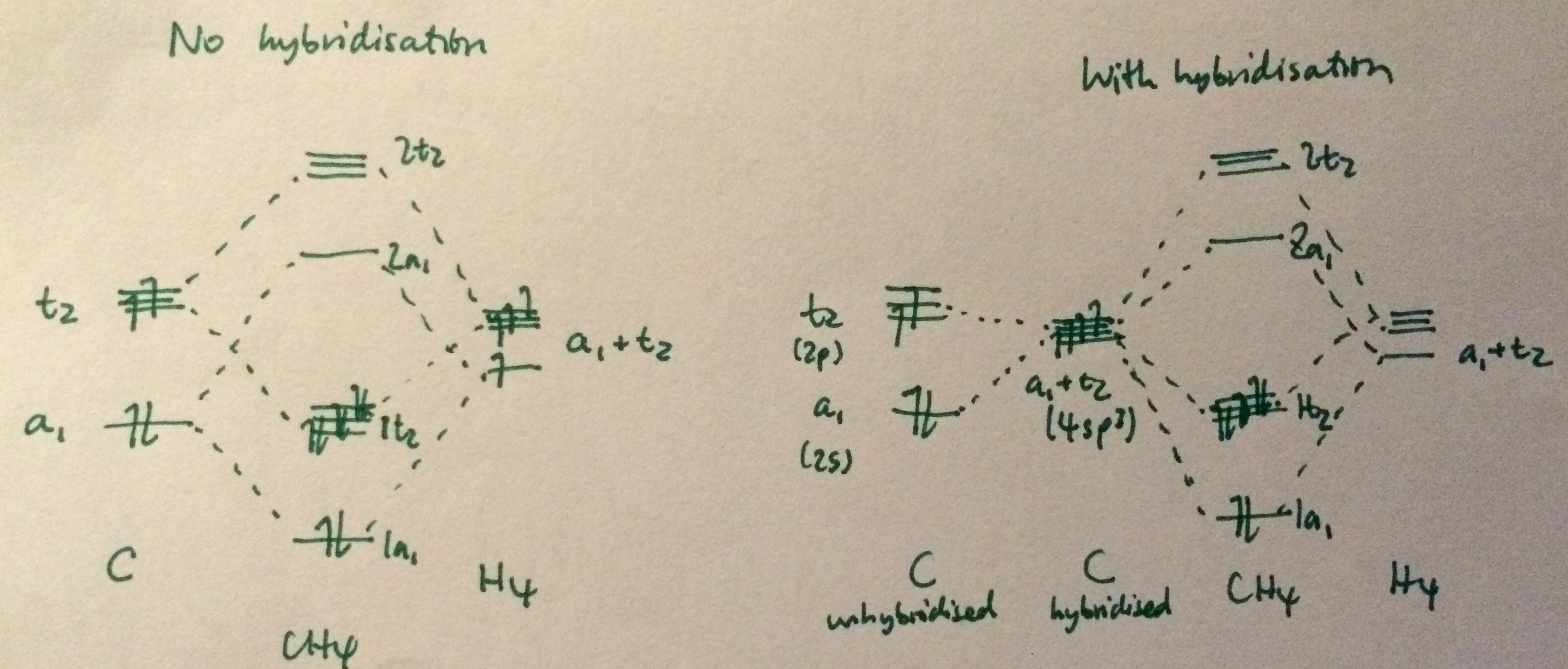
יש הבדל בין תאוריית ה- VB המקובלת. תיאוריית ה- VB המקובלת אומרת לנו שכל אחת מסלולי $ \ mathrm {sp ^ 3} $ חופפים לאחד ממסלולי המימן $ \ mathrm {1s} $ ויוצרים ארבעה קשרים זהים. ברגע שאתה מצייר דיאגרמת MO, המלאה בסימטריות, אתה נכנס לתחום של תיאוריית MO. כשאתה מגיע למולקולות גדולות יותר וצריך לחבר רסיסים שונים של המולקולה, יש הבדל בין LCAO באמצעות האורביטלים הכלאיים והלא-הכלאיים. הדוגמה הטובה ביותר היא תרשים ה- MO הראשון שציירת - אני לא יכול לדעת מה זה, אבל אני חושב שזה של אלקן. אז בואו ניקח בחשבון אתן, $ \ ce {C2H4} $.
למעשה, התרשים הוא "שגוי" . ישנם 8 אלקטרונים בסך הכל ב- AOs המרכיבים, אך ל- MOs יש רק 4 אלקטרונים. זה לא בגלל שום טעות אלמנטרית של המורה שלך. הסיבה לכך היא ששניים ממסלולי $ \ mathrm {sp ^ 2} $ בכל פחמן אינם מכוונים זה לזה; הם מצביעים לעבר המימנים במקום. לכן, הם מניחים כי הם מעורבים רק בקשירת C-H ולא בקשירת C-C. באופן קפדני, לכן הם לא צריכים להיות מוצגים בתרשים MO. עם זאת, ההנחה הזו היא שנותנת לנו קצת תובנה לגבי ההבדל בין טיפול "הכלאה-LCAO" זה לבין טיפול LCAO רגיל באמצעות AOs טהורים.
ראשית נסתכל על ה- MO האמיתיים של אתן (תמונה לקוחה מפלמינג, אורביטלים מולקולריים ותגובות כימיות אורגניות ):
$ \ hspace {15 mm} $ 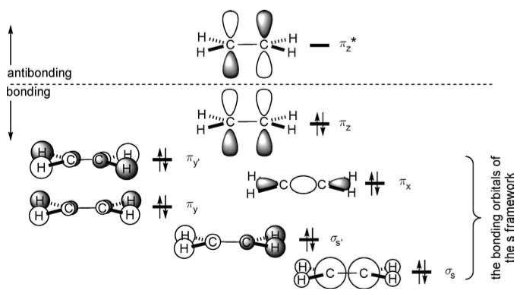
אנחנו יכולים לנסות וצייר כמה הקבלות בין דיאגרמת ה- MO "הפשטנית" שלך לתרשים ה- MO "הנכון" הזה כאן. בתרשים הפשטני, הקשר C-C $ \ sigma $ נובע מחפיפה של שני מסלולי ההיבריד $ $ \ mathrm {sp ^ 2} $. לכן, סביר להניח שזה תואם במקצת ל- $ \ pi_x $ MO לעיל, איזה סוג נראה כמו מה שאתה מצפה מחפיפה קונסטרוקטיבית של מסלולי $ \ mathrm {p} $ על פחמן המכוון זה לזה. עם זאת, סביר להניח שיש מעט מה- $ \ sigma_s $ MO מעורבבים בזה, מכיוון שאתה משתמש במסלול $ היברידי $ \ mathrm {sp ^ 2} $ שבו גם מעורבב מסלול $ \ mathrm {s} $. סביר להניח ש- MOs מלאים אחרים לא יתרמו מכיוון שהם נוגדים התנגדות ביחס לשני הפחמנים. למעשה, הם בעיקר שם כדי לספק את הקשר C-H הנוסף הנדרש כדי להפוך את המולקולה ליציבה, וזה בדיוק מה שנזנח בתרשים הפשטני.
עם זאת, מסלול ההתחברות $ \ pi $ בתרשים הפשטני שלך הוא הצלחה מסחררת. זה בדיוק כמו $ \ pi_z $ MO בתרשים האמיתי! והמסלול $ \ pi ^ * $ נוגד הקשרים בתרשים הפשטני גם הוא זהה למסלול $ \ pi_z ^ * $ בתרשים האמיתי! זה מוביל אותנו לנקודה העיקרית: אנו יכולים לעשות טיפול MO זה הרבה יותר פשוט באמצעות אורביטלים היברידיים ולקבל תמונת MO מדויקת מספיק , מבלי שנצטרך לעבור חבורה של טיעוני סימטריה כדי לקבוע אילו AOs חופפים ו אשר AOs לא. יתר על כן, נחשו אילו הם ה- MO החשובים ביותר השולטים בתגובתיות של אתן? בְּדִיוּק; זה שני המסלולים של $ \ pi $.
עכשיו כשסירתי את זה מהדרך, אני יכול להמשיך לענות על השאלות הספציפיות שלך:
הייתי מבולבל מזה מכיוון שחשבתי שתיאוריות VB ו- MO הן שתי תיאוריות נפרדות.
מה שכתבתי לעיל חל בעיקר על הבלבול הזה. עיקר העניין הוא ש הכלאה ניתן להחיל על תורת ה- VB ולמעשה בהקשר זה אתה פוגש הכלאה לראשונה, אך הוא אינו בלעדי לתיאוריית ה- VB. אתה יכול לעשות מעט mix-and-match על מנת לפשט את חייך, מבלי להקריב יותר מדי דיוק.
האם מסלולים מולקולריים נוצרים מאטום רגיל (s, p, d וכו ') אורביטלים, או שהם נוצרים גם מהאורביטלים ההיברידיים?
זו הבחירה שלך. האחת מובילה לתמונה מדויקת יותר, אך היא הופכת למייגעת ככל שהמולקולה הופכת מורכבת יותר.
ואם אורביטלים היברידיים אכן משתלבים ויוצרים אורביטלים מולקולריים, האם האלקטרונים עדיין נמצאים בין שניהם קשורים אטומים או שהם מוקדים מחדש כמו בתורת MO?
האלקטרונים ממוקמים. הדבר בולט ביותר מההבדל במסלולי $ \ sigma $ המוצגים לעיל. תיאוריית MO "נכונה" של דה-לוקליזציה a la מרמזת על כך שיש MOs המובילים לקשר על כל המולקולה, כלומר מסלול $ $ sigma_s $.
ואז מדוע אתה עדיין מכנה זאת תיאוריית MO אם האלקטרונים ממוקמים?! ?? !! ??!
לא שאלת את השאלה הזו, אבל ציפיתי שאתה יכול לתהות לגבי זה, מאז שאני ממשיך וממשיך בערך MOT רק כדי בסופו של דבר לומר שהאלקטרונים הם מקומיים. זו עדיין תיאוריית LCAO-MO, רק שמערכת הבסיס של האורביטלים שנבחרה היא שונה, מה שמוביל לצורה אחרת של פונקציית הגל שבמקרה ממוקמת בין שני גרעינים. במונחים של התפלגות צפיפות האלקטרונים זו אותה תמונה איכותית שצוברת על ידי תורת ה- VB. אך זכרו שלתיאוריית ה- VB אין מושג מהו מסלול נוגד קשרים, או שהוא בכלל קיים. אז מה שעשית הוא: למעשה הגעת לאותה תוצאה (צפיפות אלקטרונים מקומית) על ידי אמצעי אחר (MOT).
הצהרת אחריות: ישנם אנשים שיתווכחו בדיוק מהן תיאוריות "VB" ו- "MO". תפקודי גל קיימים גם בתיאוריית ה- VB, אלא שהם בנויים בצורה שונה, ואפשר מאוד לומר שתיאוריית ה- MO הפשטנית לעיל היא, למעשה, תאוריית ה- VB. עם זאת, אני מקפיד על תפישות ההיכרות והאיכותיות של תיאוריית VB ו- MO כאן. Sup>